"多重共線性"に要注意！重回帰分析で初心者が犯しがちな重大ミス

はじめに：なぜ「重回帰分析」は便利であり、同時に危ういのか？

ビジネスにおける意思決定や戦略立案において、データをもとに因果関係を読み解くことは不可欠です。その中でも「重回帰分析」は、多変量の要因がどのように結果に影響を与えるかを評価できるため、非常に有用な統計手法として広く利用されています。しかし、その便利さゆえに、分析者が“思考停止”してしまう危険性もあります。

特に「多重共線性（Multicollinearity）」という落とし穴は、分析結果の解釈を誤らせ、ビジネスにおいて誤った判断を招くリスクを孕んでいます。このコラムでは、多重共線性とは何か、なぜ問題となるのか、どのように検出し、どう対処すればよいのかを、具体例を交えてわかりやすく解説します。

多重共線性とは？ 分析の土台が揺らぐリスク

重回帰分析では、複数の説明変数（要因）が目的変数（結果）に与える影響度を「回帰係数」として定量的に示します。ところが、説明変数同士に強い相関関係がある場合、モデルの計算上の安定性が損なわれ、回帰係数の推定値が不安定になります。これが「多重共線性」が起きている状態です。結果として、本来は重要でない変数が過大評価されたり、重要な変数が過小評価されるといった事態が起こり、モデルの解釈や予測精度に大きなバイアスが生じます。

具体例：家の価格と面積・部屋数の関係

多重共線性の例としてよく挙げられるのが、「不動産価格の決定要因」に関する分析です。たとえば、「家の総面積」と「部屋の数」の2つを説明変数とし、不動産価格を目的変数として重回帰分析を行ったとします。この2つの変数は、直感的にも相関が強いことがわかります。一般的に面積が広ければ、自然と部屋数も多くなる傾向があるからです。

このように説明変数同士に強い相関関係が存在する場合、モデルはどちらの変数の影響をどう評価すべきか混乱し、たとえば「部屋数が価格に大きく影響している」と誤って結論づけてしまう可能性があります。しかし実際には、部屋数そのものよりも、面積の広さが価格に効いているのかもしれません。

多重共線性の検出方法：予防こそ最良の対策

多重共線性の存在を見抜くためには、以下のような指標や方法が役立ちます。

• 相関係数マトリクスの確認
  ⇒説明変数間で相関係数が0.8以上など、高い値を示している場合は注意が必要です。
• VIF（Variance Inflation Factor、分散拡大係数）
  ⇒各変数が他の変数によってどの程度説明されているかを示す指標。一般に、VIFが10を超える場合は多重共線性が強いとされます。
• 特異値分解や固有値の分析
  ⇒行列の条件数が大きすぎる場合、変数間の線形従属性が高いと判断されます。

多重共線性への対処法：適切な変数選択と手法の見直し

多重共線性が検出された場合、次のような対処法が考えられます。

• 相関の高い変数を削除する

  直感的で最もシンプルな手法です。ただし、意味のある変数まで削除してしまうリスクがあるため、慎重に判断する必要があります。

• 主成分分析（PCA）などの次元削減

  説明変数同士の相関構造を反映した主成分を用いて、共線性の影響を取り除きながら分析を行うことが可能です。

• 正則化手法（リッジ回帰・ラッソ回帰）

  重回帰分析の拡張手法であるリッジ回帰やラッソ回帰は、多重共線性を含む場合でも安定した係数推定が可能です。

• 決定木やランダムフォレストなどの非線形モデル

これらのモデルは、変数間の共線性にさほど敏感ではないため、代替手段として有効です。

ケーススタディ：マーケティング施策の効果測定における多重共線性

【背景】
ある飲料メーカーが、新商品の売上に対するマーケティング施策の効果を分析するため、以下の変数を用いて重回帰分析を実施しました。

• 売上（目的変数）
• テレビCM投下量（説明変数①）
• SNS広告費（説明変数②）
• 販促イベント実施数（説明変数③）

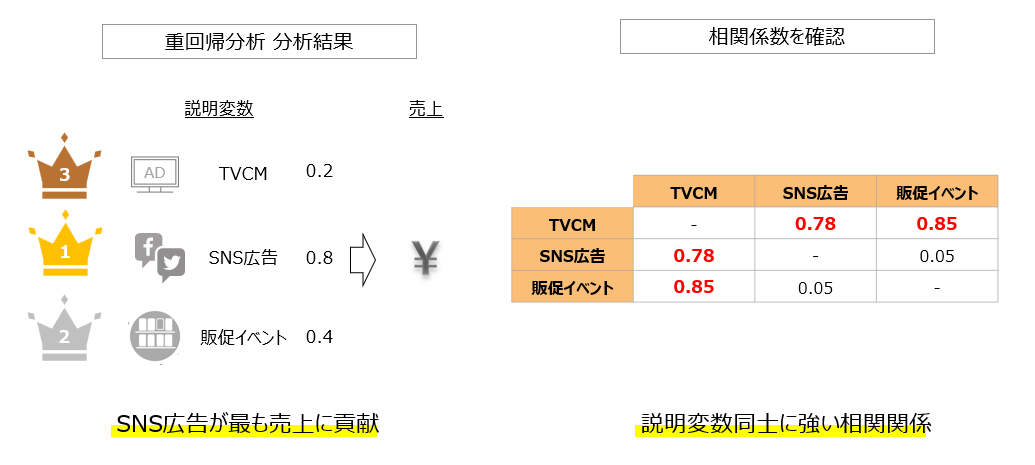
【初期の分析結果】
3つの施策すべてに有意な正の効果があると分析されました。とくに、SNS広告費の回帰係数が最も大きく、「SNS広告が最も売上に貢献している」という解釈が導かれそうになりました。

しかし…実は多重共線性の影響？
よく調べてみると、以下のような事実が判明。

• テレビCMと販促イベントは、同時期に集中的に実施されていた（相関係数：0.85）
• SNS広告費も、CM投下量と強い相関があった（相関係数：0.78）

その結果、「SNS広告が売上に効いている」と見えたのは、実際にはテレビCMやイベントによる相乗効果だった可能性が高いと判明。つまり、変数間の相関を無視していたことで、分析解釈を見誤る寸前だったのです。

【再分析】
以下の対処法により再分析が行われました。

• 変数間の相関係数行列とVIFを確認
• SNS広告費とテレビCM投下量を主成分分析で統合
• 再度、重回帰分析を実施

【最終分析結果】
販促イベントの効果が最も顕著であり、テレビCMやSNSは単独ではなく「複合的な接触効果」として売上に影響していると解釈されました。

最後に：分析は「技術」ではなく「姿勢」

多重共線性の問題は、分析者の技術的な理解の深さに加え、「結果をうのみにしない」という姿勢が問われるテーマです。どれだけ精緻なモデルを組んでも、元のデータ構造や変数の関係性を無視してしまえば、誤った意思決定に直結してしまいます。

特に、ビジネス現場においては、「解釈可能性」や「納得感」のある結果が求められるため、数値の裏側にある構造を丁寧に読み解く姿勢が不可欠です。「多重共線性」という一見専門的な問題も、実は分析全体の“土台”に関わる本質的な課題です。この課題に真摯に向き合うことが、信頼されるデータ分析者への第一歩といえるでしょう。

MyStoryでは、重回帰分析をもとにした計量経済学モデルでのビジネス支援実績が豊富にあります。複雑な構造を持つデータにおいても、多重共線性を正しく扱い、正確な分析結果をご提供することが可能です。ご相談をご希望される方は、お問い合わせページより気軽にご連絡ください。